This is where navigation should be.
DEMO_WAVELETS - Wavelet filter banks
Description
This demo exemplifies the use of the wavelet filter bank trees. All representations use "least asymmetric" Daubechies wavelet orthonormal filters 'sym8' (8-regular, length 16).
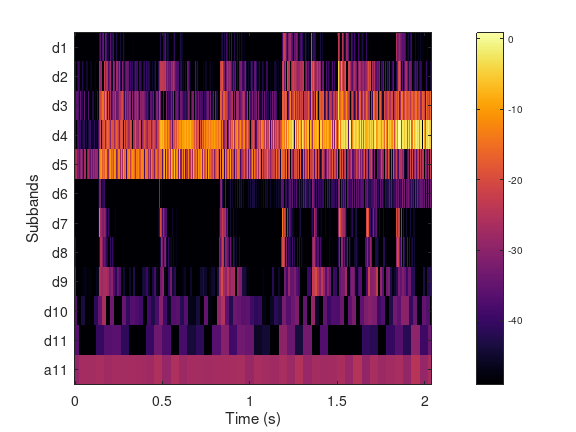
DWT representation
The filter bank tree consists of 11 levels of iterated 2-band basic
wavelet filter bank, where only the low-pass output is further
decomposed. This results in 12 bands with octave resolution.
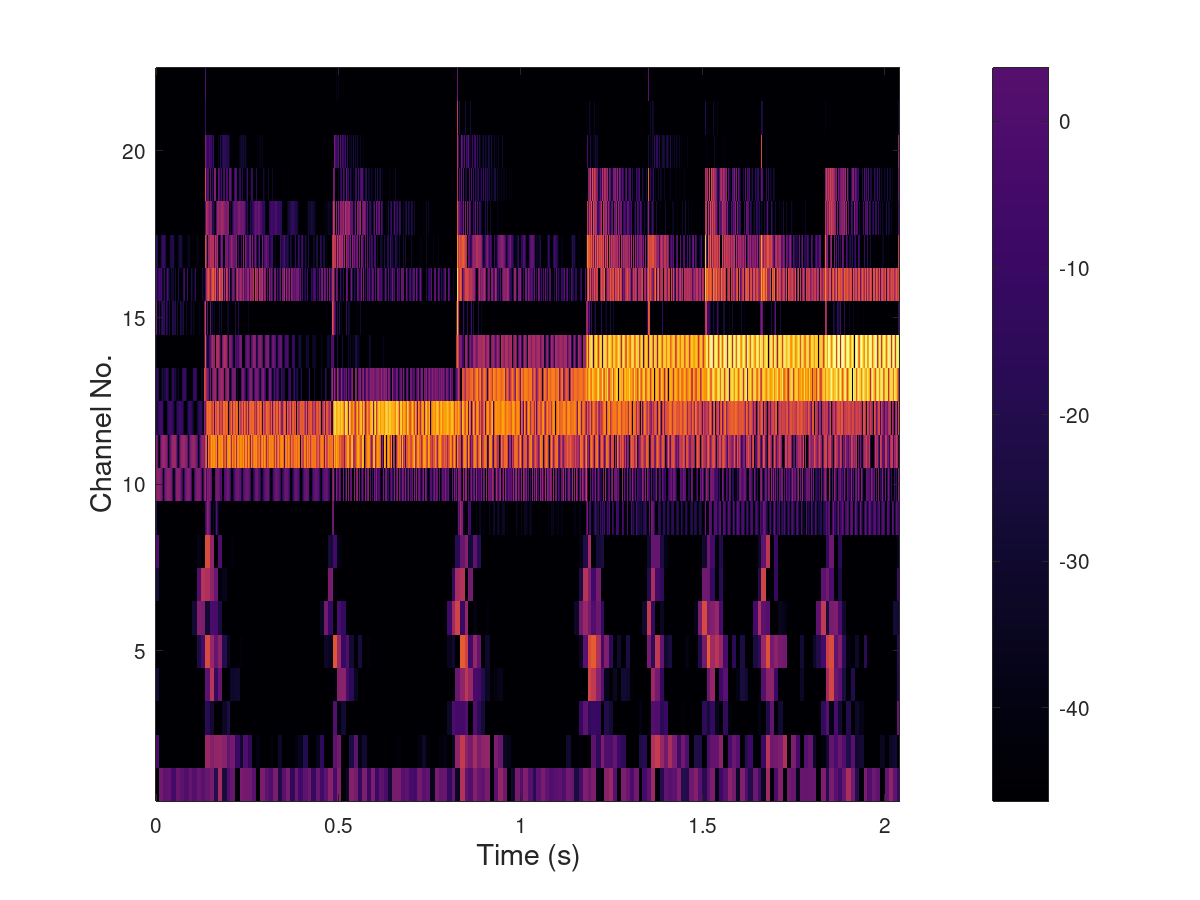
8-band DWT representation
The filter bank tree (effectively) consists of 3 levels of iterated
8-band basic wavelet filter bank resulting in 22 bands. Only the
low-pass output is decomposed at each level.
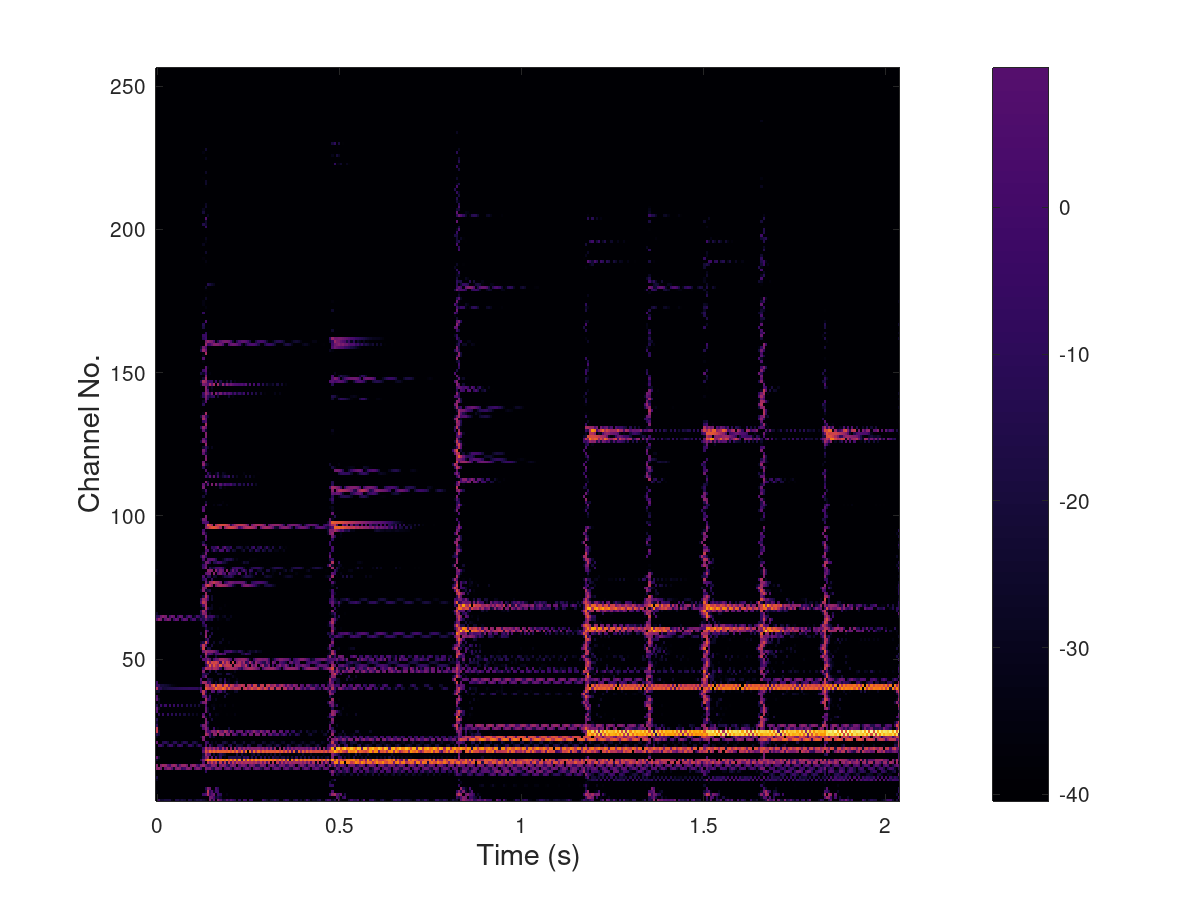
Full Wavelet filter bank tree representation
The filter bank tree depth is 8 and it is fully decomposed meaning
both outputs (low-pass and high-pass) of the basic filter bank is
plot further. This results in 256 bands linearly covering the
frequency axis.
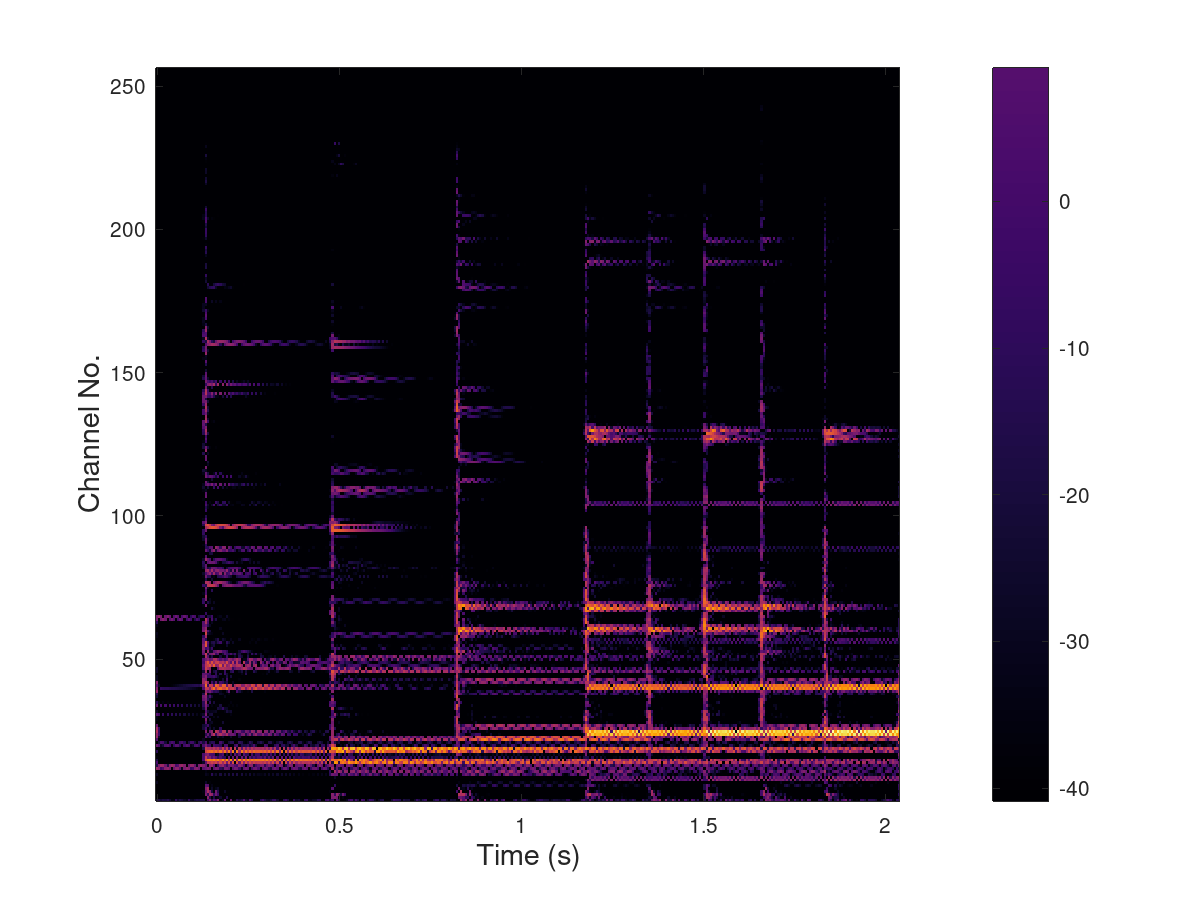
Full Wavelet filter bank tree representation
The same case as before, but symmetric nearly orthogonal basic
filter bank is used.
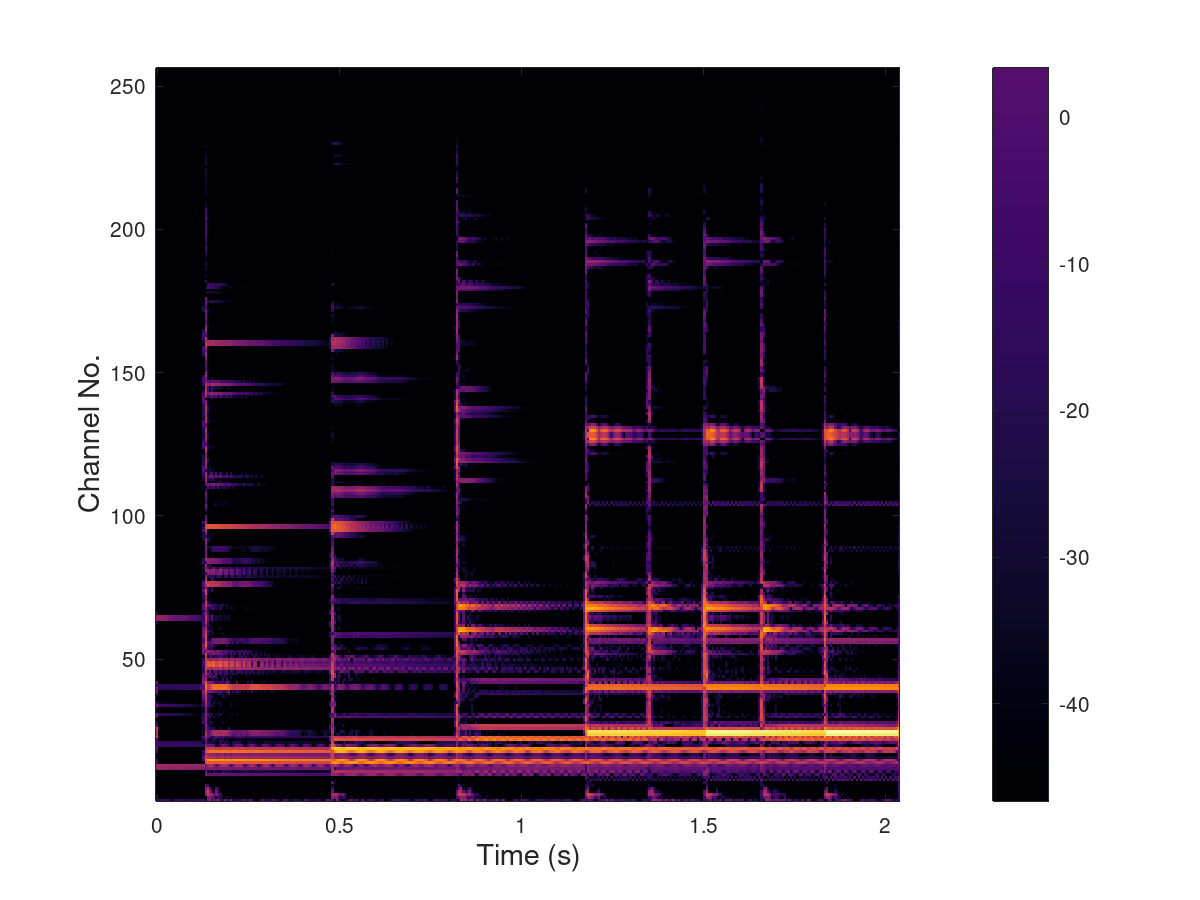
Full Dual-tree Wavelet filter bank representation
This is a 2 times redundant representation using Q-shift dual-tree
wavelet filters.