DEMO_PHASEPLOT - Give demos of nice phaseplots
Description
This script creates a synthetic signal and then uses phaseplot on it, using several of the possible options.
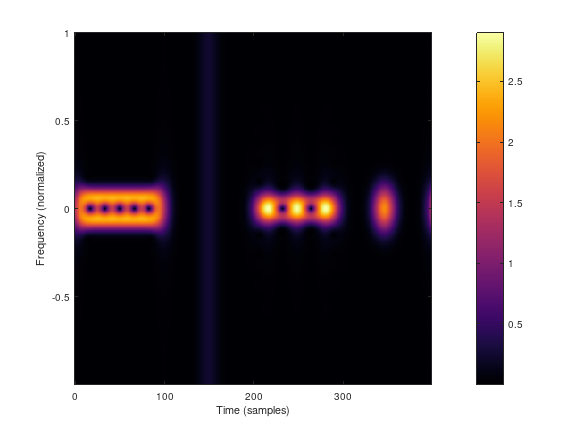
For real-life signal only small parts should be analyzed. In the chosen demo the fundamental frequency of the speaker can be nicely seen.
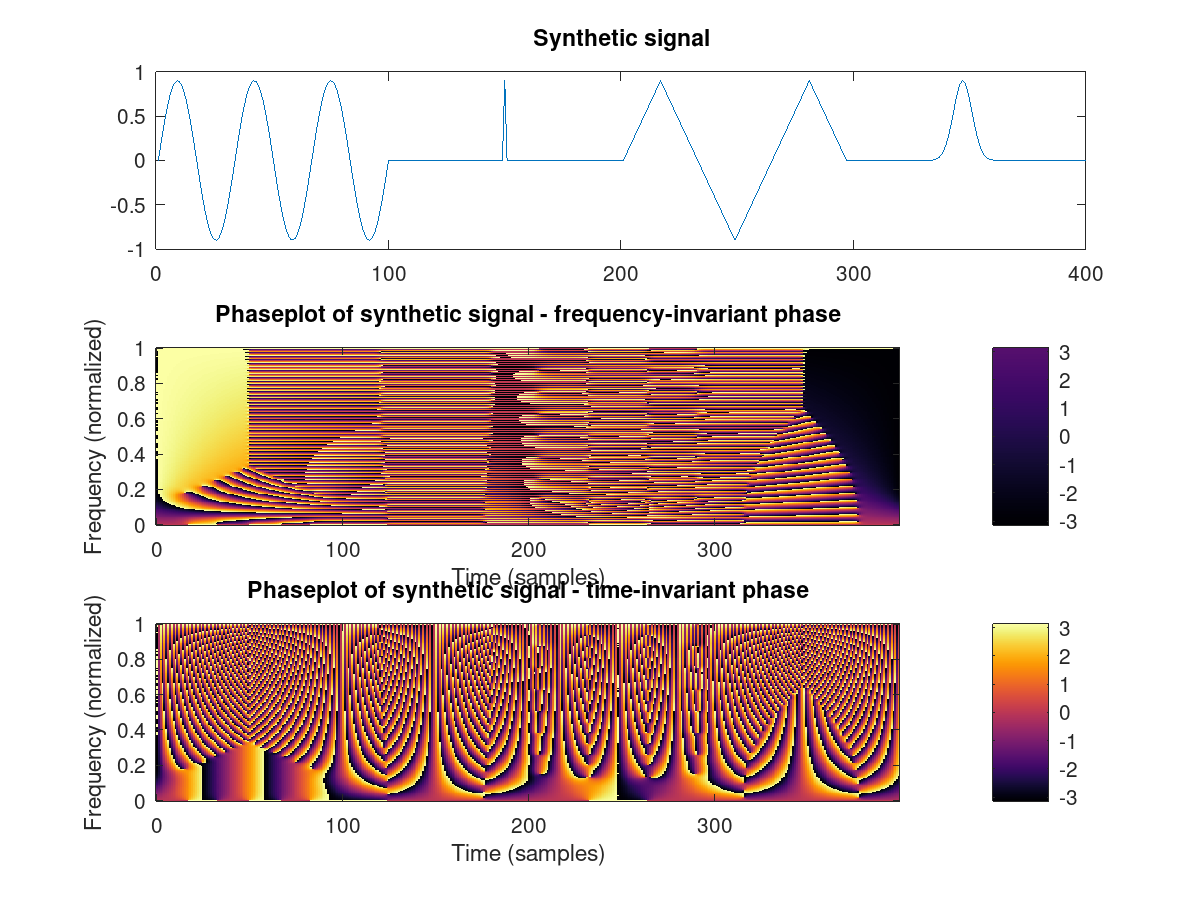
Synthetic signal
Compare this to the pictures in reference 2 and 3. In the first two figures a synthetic signal is analyzed. It consists of a sinusoid, a small Delta peak, a periodic triangular function and a Gaussian. In the time-invariant version in the first part the periodicity of the sinusoid can be nicely seen also in the phase coefficients. Also the points of discontinuities can be seen as asymptotic lines approached by parabolic shapes. In the third part both properties, periodicity and discontinuities can be nicely seen. A comparison to the spectogram shows that the rectangular part in the middle of the signal can be seen by the phase plot, but not by the spectogram.
In the frequency-invariant version, the fundamental frequency of the sinusoid can still be guessed as the position of an horizontal asymptotic line.
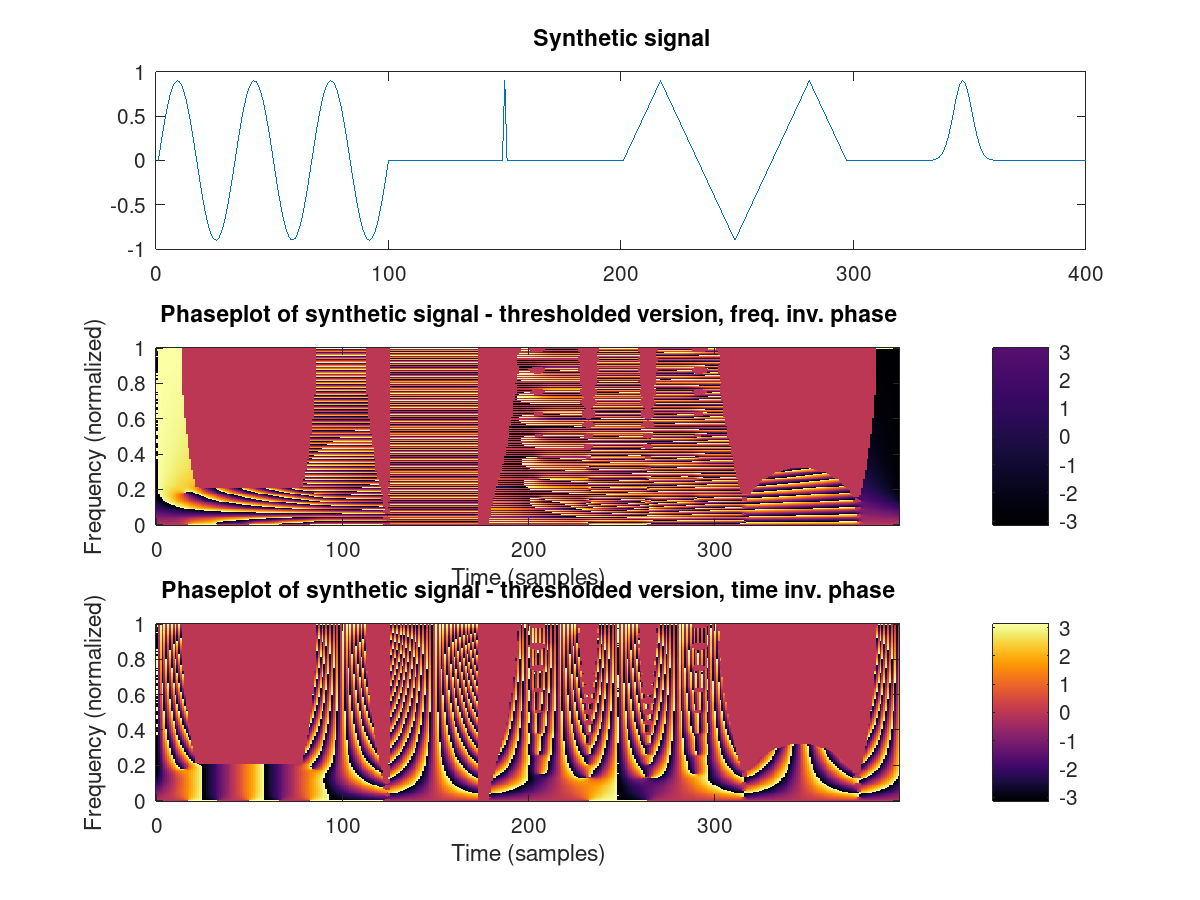
Synthetic signal, thresholded.
Speech signal.
References:
R. Carmona, W. Hwang, and B. Torrésani. Multiridge detection and time-frequency reconstruction. IEEE Trans. Signal Process., 47:480--492, 1999.
R. Carmona, W. Hwang, and B. Torrésani. Practical Time-Frequency Analysis: continuous wavelet and Gabor transforms, with an implementation in S, volume 9 of Wavelet Analysis and its Applications. Academic Press, San Diego, 1998.
A. Grossmann, M. Holschneider, R. Kronland-Martinet, and J. Morlet. Detection of abrupt changes in sound signals with the help of wavelet transforms. Inverse Problem, pages 281--306, 1987.